Архівний відеоурок ?

Рекомендований підручник: 

1) Алгебра* (академічний, профільний рівень) (підручник) Нелін Є.П., Долгова О.Є.

2) Математика* (рівень стандарту) (підручник) Бевз Г.П., Бевз В.Г.

Читати:

1) Параграф 5, стор. 46 - 91

2) Параграф 10, стор. 78 - 90

Головне в уроці:

Похідна – важливий інструмент дослідження функцій. Наприклад, завдяки похідній можна дослідити функцію на монотонність.

Внутрішні точки області визначення функції, в яких функція неперервна, а похідна дорівнює нулю або не існує, називають критичними точками (іноді використовується поняття стаціонарні точки – це внутрішні точки області визначення функції, в яких функція неперервна, а похідна дорівнює нулю).

Ці точки дуже важливі для аналізу функції та побудови її графіку, бо лише в цих точках функція може маті екстремум.

Точка екстремуму (мінімуму/максимуму) – це точка, в якій досягається максимальне або мінімальне значення функції на деякому проміжку.

Достатня умова екстремуму:

Якщо похідна при переході через критичну точку x₀ змінює знак з плюсу на мінус, то x₀  – точка максимуму.

Якщо похідна при переході через критичну точку x₀  змінює знак з мінусу на плюс, то x₀ – точка мінімуму.

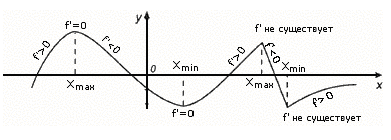
Схема дослідження функції y = f(x) на монотонність та екстремум.

1. Знайти область визначення функції.

2. Знайти похідну f '(x) .

3. Знайти критичні точки.

4. Знайти знак похідної на кожному з інтервалів, на які розбивають критичні точки область визначення, а також визначити характер поведінки функції на них.

5. Визначити, чи є критичні точки точками екстремуму. Знайти значення у точках екстремуму.

Приклад повного дослідження функції:

y = -x³ + 3x² + 5

Знайдемо область визначення функції:

D (y) = R

Знайдемо похідну функції:

y ' = -3x² + 6x

Знайдемо критичні точки функції:

Похідна визначена у всіх точках, знайдемо ті, у яких вона дорівнює нулю.

-3x² + 6x =  0

-3x(x - 2) = 0

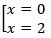
Відмічаємо критичні точки на числовій осі:

Ці точки розбивають область визначення на три інтервали, визначимо знак похідної на кожному з них:

Точка 0 – точка мінімуму, точка 2 – точка максимуму. Знайдемо значення у точках екстремуму:

y(0) = 0 + 0 + 5 = 5

y(2) = -8 + 3 • 4 + 5 = 9

Запишемо отримані дані в таблицю:

Побудуємо ескіз графіка функції:

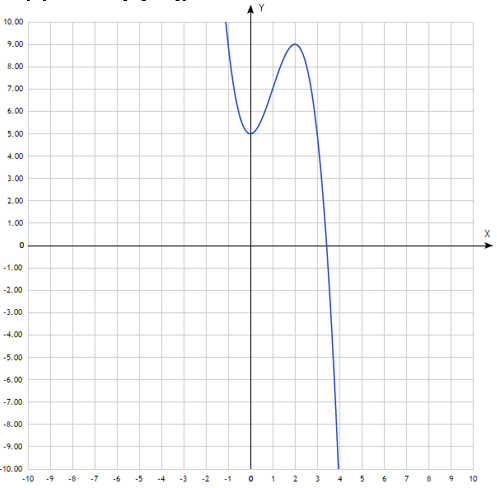
Як досліджувати функцію та будувати її графік?

Монотонність функції та її зв’язок з похідною

Поняття екстремуму функції

Найбільше та найменше значення функції, неперервної на відрізку

Дослідження функції та побудова її графіка